Serialization

Catalogue

1. 1. Tree String
   1. 1.1. 297. Serialize and Deserialize Binary Tree
2. 2. Tree Serialization
   1. 2.1. 426. Convert Binary Search Tree to Sorted Doubly Linked List
3. 3. Tree De-Serialization
   1. 3.1. 106. Construct Binary Tree from Inorder and Postorder Traversal
   2. 3.2. 105. Construct Binary Tree from Preorder and Inorder Traversal
   3. 3.3. Construct Binary Tree from Inorder and level Order
   4. 3.4. 114. Flatten Binary Tree to Linked List

Tree <-> String

When you use network to transport a tree or a graph, you can not pass the momery. So usually you have to use a string to transport!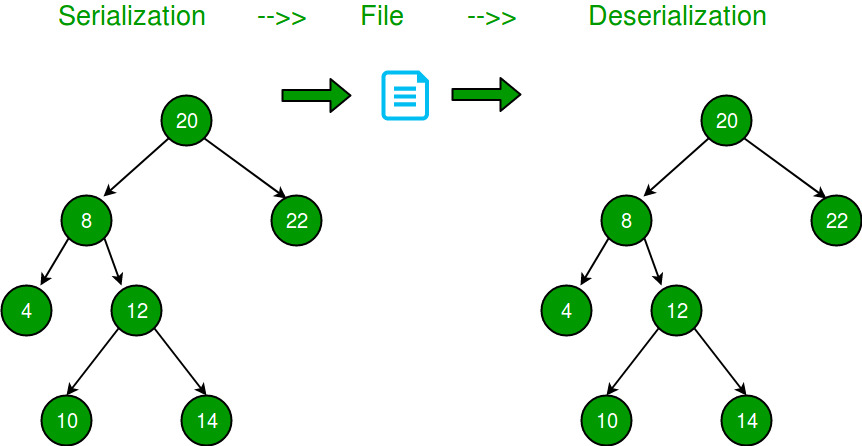

• Binary Search Tree
• Complete Tree
• Full Tree

  297. Serialize and Deserialize Binary Tree

  class Codec:
      def serialize(self, root):
          res = []
          def dfs(node):
              if not node:
                  res.append("None")
                  return
  
              res.append(str(node.val))
              dfs(node.left)
              dfs(node.right)
          dfs(root)
          return ','.join(res)
  
  
  
      def deserialize(self, data):
          def helper(q):
              if tokens[0] == "None":
                  q.popleft()
                  return None
              root = TreeNode(q.popleft())
              root.left = helper(q)
              root.right = helper(q)
              return root
  
          tokens = collections.deque(data.split(','))
          root = helper(tokens)
          return root

Tree Serialization

426. Convert Binary Search Tree to Sorted Doubly Linked List

• O(n) extra space

  # Time : O(n), Space : O(n)
  class Solution(object):
      def treeToDoublyList(self, root):
          if not root:
              return None
  
          res = []
          self.inOrder(root, res)
          n = len(res)
          for i in xrange(n):
              res[i].right = res[i+1] if i < n-1 else res[0]
              res[i].left = res[i-1]
          return res[0]
  
      def inOrder(self, root, res):
          if not root:
              return
          self.inOrder(root.left, res)
          res.append(root)
          self.inOrder(root.right, res)

• in-place

  # Time : O(n), Space : O(1)
  class Solution(object):
      def treeToDoublyList(self, root):
          if not root:
              return None
  
          self.prev = None
          self.head = None
          self.inOrder(root)
          self.prev.right = self.head
          self.head.left = self.prev
          return self.head
  
      def inOrder(self, root):
          if not root:
              return
          self.inOrder(root.left)
          if self.prev:
              root.left = self.prev
              self.prev.right = root
          else:
              self.head = root
          self.prev = root
          self.inOrder(root.right)

Tree De-Serialization

• We can NOT construct a Binary Tree using postorder and preorder

106. Construct Binary Tree from Inorder and Postorder Traversal

• Global Question divide to sub problem

class Solution(object):
    def buildTree(self, inorder, postorder):
        if not inorder or not postorder:
            return None

        root = TreeNode(postorder.pop())
        inorderindex = inorder.index(root.val)
        root.right= self.buildTree(inorder[inorderindex+1:], postorder)
        root.left = self.buildTree(inorder[:inorderindex], postorder)

        return root

105. Construct Binary Tree from Preorder and Inorder Traversal

class Solution(object):
    def buildTree(self, preorder, inorder):
        if (not preorder) or (not inorder):
            return None
        root=TreeNode(preorder.pop(0))
        ro=inorder.index(root.val)
        root.left=self.buildTree(preorder,inorder[:ro])
        root.right=self.buildTree(preorder,inorder[ro+1:])
        return root

Construct Binary Tree from Inorder and level Order

114. Flatten Binary Tree to Linked List

class Solution(object):
    def flatten(self, root):
        if not root:
            return

        if not root.left:
            self.flatten(root.right)
            return

        self.flatten(root.left)
        self.flatten(root.right)

        cur = root.left
        while cur.right:
            cur = cur.right
        cur.right = root.right
        root.right = root.left
        root.left = None