pramp

Catalogue

1. 1. Communication
   1. 1.1. small talk
   2. 1.2. interviewer
   3. 1.3. interviewee
2. 2. Tree
   1. 2.1. Sales Path
   2. 2.2. BST Successor Search
3. 3. Other
   1. 3.1. H-Tree Construction
   2. 3.2. Getting a Different Number
   3. 3.3. Array Index & Element Equality
   4. 3.4. Number of Paths
      1. 3.4.1. Explanation
   5. 3.5. Sentence Reverse
   6. 3.6. Matrix Spiral Copy

Communication

• diagram

small talk

• How are you? Im doing great!
• Thank you for the interview!
• Have a good night! / Have a nice day!

interviewer

• can you hear me?
• can i assume that … ?
• walk through a small example / some test cases
• It looks good for me / Sounds good!
• Im not sure why you … ?
• in the line …
• can you analyze the time and space complexity?
• the question said that …
• there are some typo in your code
• clarify your idea
• I will be the interviewer fist
• make sense / make no sense
• on the right track
• you get the point!
• you can use either BFS or DFS
• Go ahead!

interviewee

• Let me give you a small example
• double check my code
• write some test cases to test my funciton
• as we can see
• analyze different cases first
• Lets say … variable …
• Can you share a small example for me?
• make sure that i understand the question!

Tree

• can we assume that class node has parent pointer?

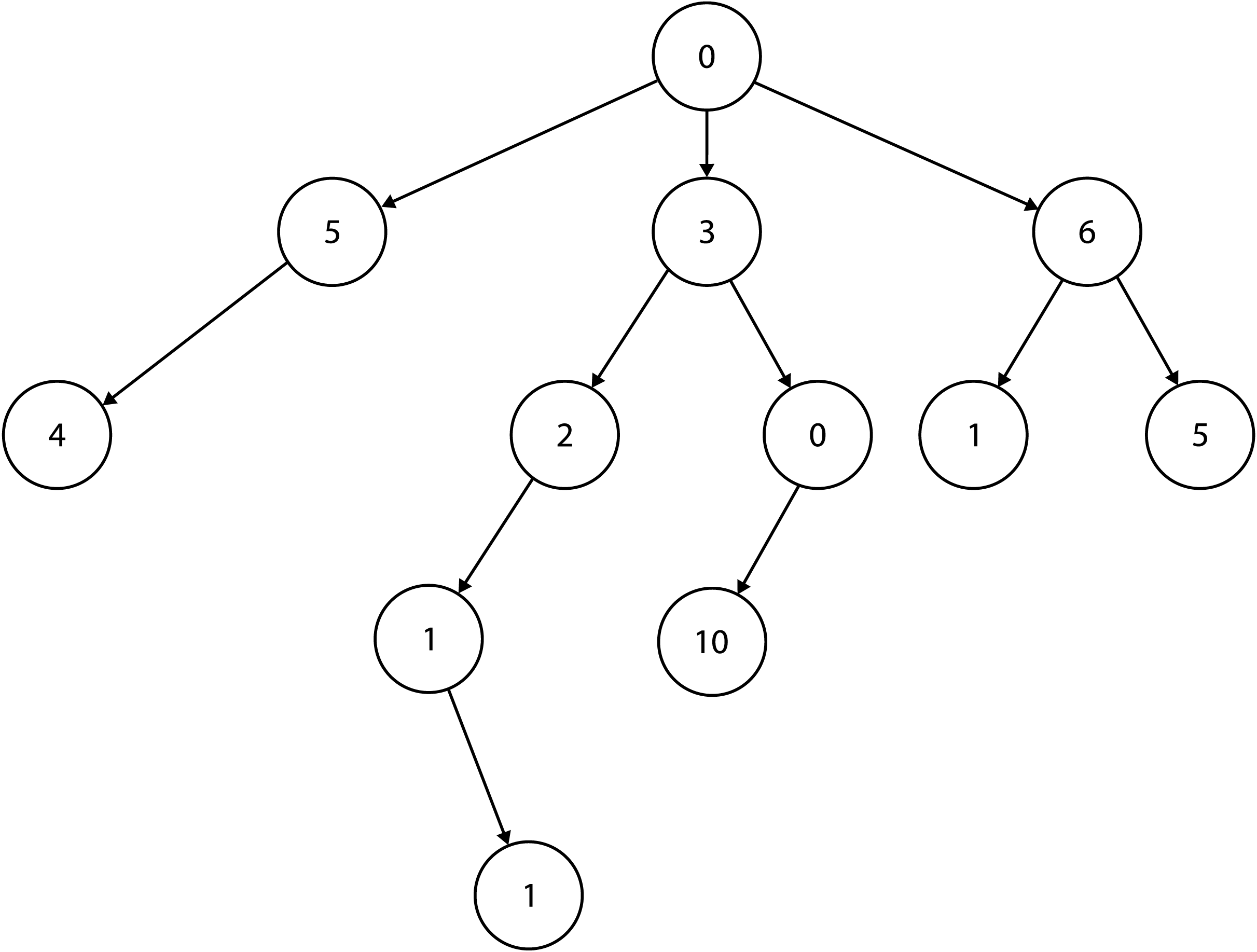
Sales Path

• Find the minimal sum cost from root to leaf in a Tree (Not necessarily binary)

  

  # Time : O(n), Space : O(n)
  def get_cheapest_cost(rootNode):
    if not rootNode.children:
      return rootNode.cost
  
    minCost = float('inf')
    for child in rootNode.children:
      minCost = min(minCost, get_cheapest_cost(child))
    return minCost + rootNode.cost

• follow up:
  TODO

BST Successor Search

In a Binary Search Tree (BST), an Inorder Successor of a node is defined as the node with the smallest key greater than the key of the input node (see examples below).

Given a node inputNode in a BST, you’re asked to write a function findInOrderSuccessor that returns the Inorder Successor of inputNode. If inputNode has no Inorder Successor, return null.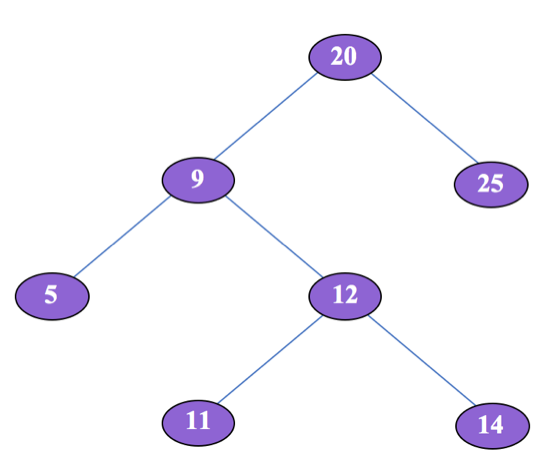

def find_in_order_successor(self, inputNode):
  if not inputNode:
    return None

  if not inputNode.right: # dose not have right subtree
    parent = inputNode.parent
    if not parent: # root node
      return None
    while parent:
      if parent.key > inputNode.key:
        return parent
      parent = parent.parent
    return None
  else:# have right subree
    cur = inputNode.right
    while cur.left:
      cur = cur.left
    return cur

1. Case1 : inputNode has a right child. In this case successorNode would be the node with the minimum key in inputNode’s right subtree.

2. Case2: inputNode doesn’t have a right child. In this case successorNode would be one of inputNode’s ancestors. More specifically, within inputNode’s ancestor chain (starting from inputNode all the way up to the root), successorNode is the first parent that has a left child in that chain.

Other

H-Tree Construction

Write a function drawHTree that constructs an H-tree, given its center (x and y coordinates), a starting length, and depth. Assume that the starting line is parallel to the X-axis.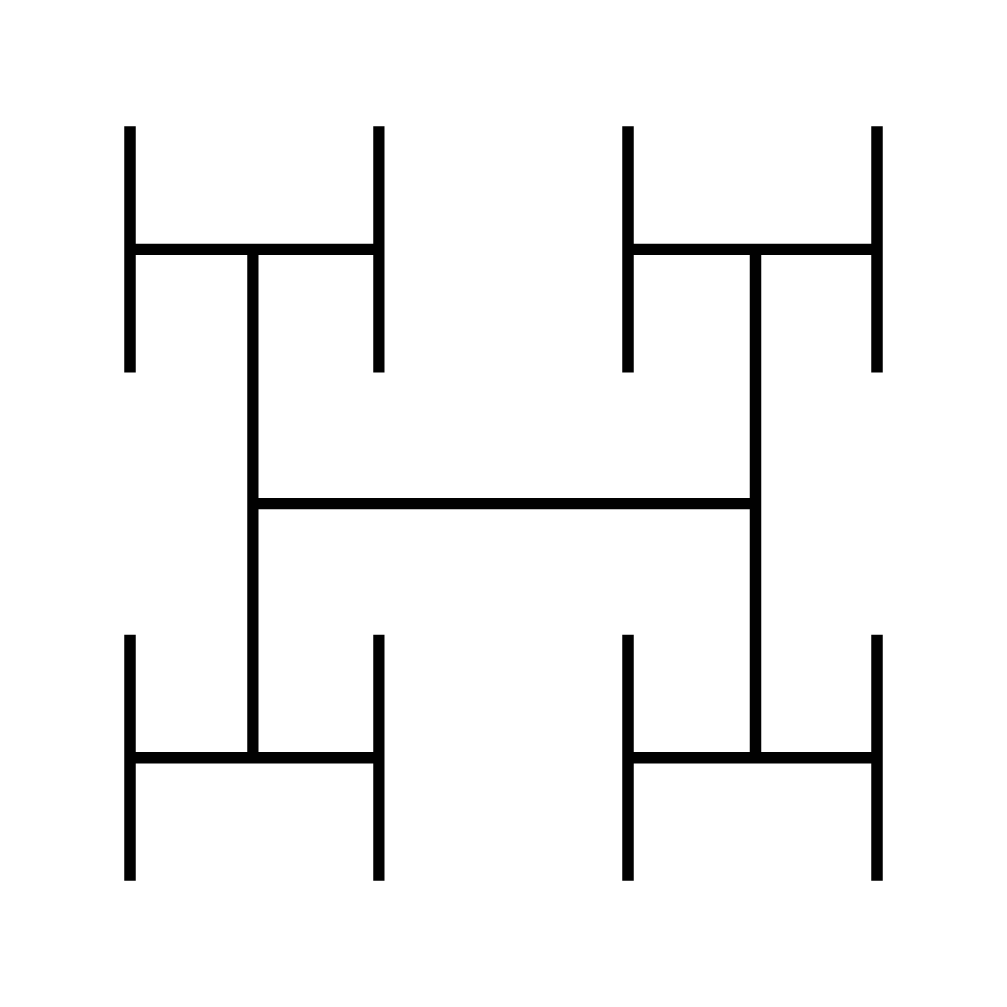

• Use the function drawLine provided to implement your algorithm. In a production code, a drawLine function would render a real line between two points. However, this is not a real production environment, so to make things easier, implement drawLine such that it simply prints its arguments (the print format is left to your discretion).

• Analyze the time and space complexity of your algorithm. In your analysis, assume that drawLine’s time and space complexities are constant, i.e. O(1).

            1
   1     1     1     1
1 1 1 1  

import math
def drawLine(p1, p2):
  # draw line

# Time : O(4^depth)
# Space : O(depth)  
def drawHTree(x, y, length, depth):
    if depth == 0:
      return

    # horizontal segment "-"
    x1 = x - length / 2
    x2 = x + length / 2
    drawLine((x1, y), (x2, y))

    # left & right vertical segment '|'
    y1 = y - length / 2
    y2 = y + length / 2
    drawLine((x1, y1), (x1, y2))
    drawLine((x2, y1), (x2, y2))

    # Recursion
    new_len = length / math.sqrt(2)
    drawHTree((x1, y1), new_length, depth - 1)
    drawHTree((x1, y2), new_length, depth - 1)
    drawHTree((x2, y1), new_length, depth - 1)
    drawHTree((x2, y2), new_length, depth - 1)

Getting a Different Number

Given an array arr of unique nonnegative integers, implement a function getDifferentNumber that finds the smallest nonnegative integer that is NOT in the array.

# Time : O(n)
# Space : O(n)
def get_different_number(arr):
  n = len(arr)
  arr_set = set(arr)
  for i in xrange(n+1):
    if i not in arr_set:
      return i

Array Index & Element Equality

Given a sorted array arr of distinct integers, write a function indexEqualsValueSearch that returns the lowest index i for which arr[i] == i. Return -1 if there is no such index.

• Binary Search
• Edge case

# Time : O(logn)
# Space : O(1)
def index_equals_value_search(arr):
  if not arr:
    return -1

  start, end = 0, len(arr)-1
  while start < end:
    mid = start + (end - start) // 2
    if arr[mid] == mid:
      end = mid
    elif arr[mid] > mid:
      end = mid - 1
    else:
      start = mid + 1

  # post processing
  if arr[start] == start:
    return start
  else:
    return -1

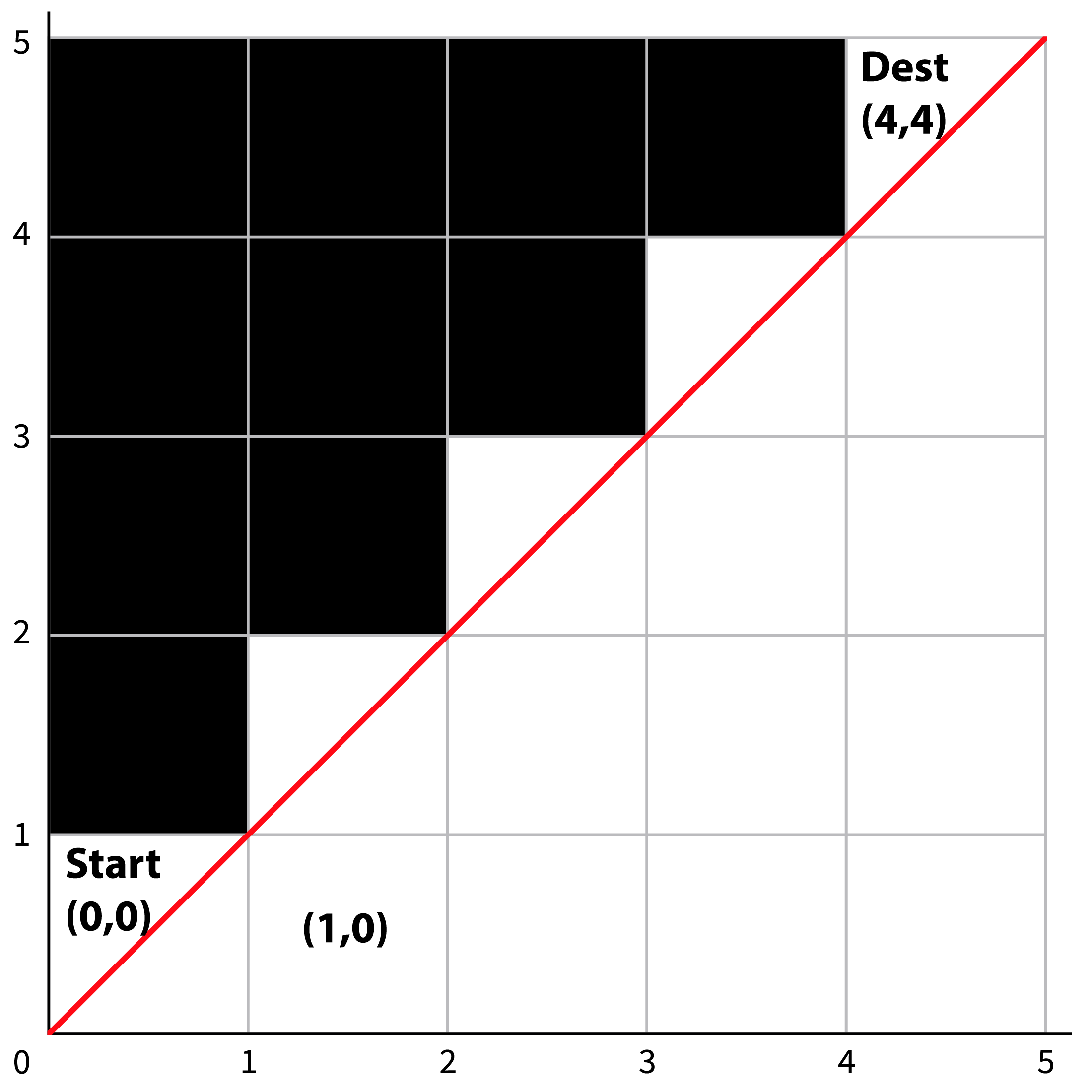
Number of Paths

Given n, the size of the grid’s axes, write a function numOfPathsToDest that returns the number of the possible paths the driverless car can take.

def num_of_paths_to_dest(n):
  # Init dp
  #dp = [[0] * n for _ in xrange(n)]
  dp = [1] * n

  # calculate the number
  for i in xrange(1, n):
    for j in xrange(i+1, n):
      dp[j] += dp[j-1]

  return dp[-1]

def test():
  print(num_of_paths_to_dest(4))

test()

# Time : O(n^2) Space : O(n^2)
# Improved Space : O(n)

Explanation

Since the car can only move up and move down, when it arrives at a point, there are two possibilities:

1. It arrives at the point from below cell (move up to the point)
2. It arrives at the point from left cell (move right to the point)

Sentence Reverse

• Solution1. python built-in function

  # Time : O(n), Spacce : O(n)
  def reverse_words1(arr):
    string = ''.join(arr)
    chs = string.split()
    res = ' '.join(chs[::-1])
    return list(res)

• Solution2. Reverse Twice

• First: reverse all the word!
  I love google -> I evol elgoog
• Second: reverse the string character by charater
  I evol elgoog -> google love I

# Space O(n) -> O(1)
def reverse_words(arr):

  # First Reverse
  start = 0
  for i in xrange(len(arr)+1):
    if i == len(arr) or arr[i] == ' ': # condition
      end = i - 1
      while start < end:
        arr[start], arr[end] = arr[end], arr[start]
        start += 1
        end -= 1
      start = i + 1

  # Second Reverse
  start, end = 0, len(arr)-1
  while start < end:
    arr[start], arr[end] = arr[end], arr[start]
    start += 1
    end -= 1
  return arr

Matrix Spiral Copy

Given a 2D array (matrix) inputMatrix of integers, create a function spiralCopy that copies inputMatrix’s values into a 1D array in a spiral order, clockwise. Your function then should return that array. Analyze the time and space complexities of your solution.

class Solution:
    def spiralOrder(self, matrix):
        if not matrix:
            return []

        m, n = len(matrix), len(matrix[0])
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        k = 0
        visited = set()
        x = y = 0
        res = []
        while len(res) < m * n:
            res.append(matrix[x][y])
            visited.add((x, y))

            dx, dy = directions[k]
            nx, ny = x+dx, y+dy
            if (nx, ny) not in visited and 0 <= nx <= m-1 and 0 <= ny <= n-1:
                x, y = nx, ny
            else: # need to change direction
                k = (k + 1) % 4
                dx, dy = directions[k]
                x, y = x+dx, y+dy
        return res