DP - Double Sequence

Catalogue

1. 1. 1 Longest
   1. 1.1. LintCode 79. Longest Common Substring
   2. 1.2. LintCode 77. Longest Common Subsequence
2. 2. 2 Exist
   1. 2.1. 10. Regular Expression Matching
   2. 2.2. 97. Interleaving String
3. 3. 3 Count
   1. 3.1. 72. Edit Distance
   2. 3.2. 161. One Edit Distance
   3. 3.3. 801. Minimum Swaps To Make Sequences Increasing

• Input Parameters have two Sequences or Strings
• Two Sequences Matching?

1 Longest

LintCode 79. Longest Common Substring

class Solution:
    def longestCommonSubstring(self, A, B):
        m, n = len(A), len(B)
        dp = [[0] * (n+1) for _ in range(m+1)]
        res = 0
        for i in range(m):
            for j in range(n):
                if A[i] == B[j]:
                    dp[i+1][j+1] = dp[i][j] + 1
                    res = max(res, dp[i+1][j+1])
        return res

LintCode 77. Longest Common Subsequence

• State : dp[i][j] means Longest Common Subsequence for A[0…i-1] and B[0…j-1]
• Init : dp[i][0] = dp[0][j] = 0
• Deduction Formula :

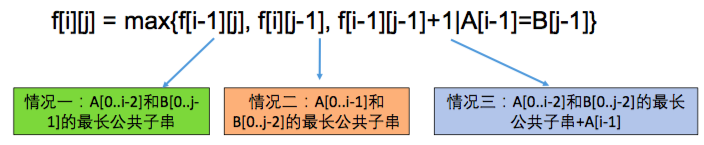
# Time : O(mn), Space : O(mn)
class Solution:
    def longestCommonSubsequence(self, A, B):
        m, n = len(A), len(B)
        if m == 0 or n == 0:
            return 0

        dp = [[0] * (n+1) for _ in xrange(m+1)]
        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                if A[i-1] == B[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        return dp[-1][-1]

• Space Improvement
  dp[i][j] -> dp[i % 2][j]

# Space : O(n)
class Solution:
    def longestCommonSubsequence(self, A, B):
        m, n = len(A), len(B)
        if m == 0 or n == 0:
            return 0

        dp = [[0] * (n+1) for _ in xrange(2)]
        for i in xrange(1, m+1):
            for j in xrange(1, n+1):
                if A[i-1] == B[j-1]:
                    dp[i % 2][j] = dp[(i-1) % 2][j-1] + 1
                else:
                    dp[i % 2][j] = max(dp[(i-1) % 2][j], dp[i % 2][j-1])
        return dp[m % 2][-1]

2 Exist

10. Regular Expression Matching

• Case Analysis!!!

  class Solution(object):
      def isMatch(self, s, p):
          m, n = len(s), len(p)
          dp = [[False] * (n+1) for _ in range(m+1)]
          dp[0][0] = True
          for i in range(n):
              if p[i] == "*":
                  dp[0][i+1] = dp[0][i-1]
  
          for i in range(m):
              for j in range(n):
                  if s[i] == p[j] or p[j] == '.':
                      dp[i+1][j+1] = dp[i][j]
                  elif p[j] == '*':
                      dp[i+1][j+1] = dp[i+1][j-1]
                      if p[j-1] == '.' or p[j-1] == s[i]:
                          dp[i+1][j+1] = dp[i+1][j+1] or dp[i][j+1]
          return dp[-1][-1]

97. Interleaving String

• Three String!!

  class Solution(object):
      def isInterleave(self, s1, s2, s3):
          m, n, l = len(s1), len(s2), len(s3)
          if m + n != l:
              return False
  
          dp = [[False] * (n+1) for _ in range(m+1)]
          dp[0][0] = True
          for i in range(m):
              if s1[i] == s3[i]:
                  dp[i+1][0] = dp[i][0]
  
          for j in range(n):
              if s2[j] == s3[j]:
                  dp[0][j+1] = dp[0][j]
  
          for i in range(m):
              for j in range(n):
                  if s3[i+j+1] == s1[i]:
                      dp[i+1][j+1] = dp[i+1][j+1] or dp[i][j+1]
                  if s3[i+j+1] == s2[j]:
                      dp[i+1][j+1] = dp[i+1][j+1] or dp[i+1][j]
          return dp[-1][-1]

3 Count

72. Edit Distance

class Solution(object):
    def minDistance(self, word1, word2):
        m, n = len(word1), len(word2)
        dp = [[0] * (n+1) for _ in xrange(m+1)]

        for i in xrange(m):
            dp[i+1][0] = i+1
        for i in xrange(n):
            dp[0][i+1] = i+1

        for i in xrange(m):
            for j in xrange(n):
                dp[i+1][j+1] = min(dp[i][j+1]+1, dp[i+1][j]+1, dp[i][j] + (word1[i] != word2[j]))
        return dp[-1][-1]

161. One Edit Distance

• a littel like “Edit Distance”, but totally different solution!!! no dp here!

class Solution(object):
    def isOneEditDistance(self, s, t):
        if len(s) < len(t):
            return self.isOneEditDistance(t, s)

        m, n = len(s), len(t)
        if m - n > 1:
            return False

        if m - n == 1:
            for i in xrange(n):
                if s[i] != t[i]:
                    return s[i+1:] == t[i:]
            return True

        if m == n:
            for i in xrange(m):
                if s[i] != t[i]:
                    return s[i+1:] == t[i+1:]
            return False

801. Minimum Swaps To Make Sequences Increasing

• State
  swap[i]: The cost of making both sequences increasing up to the first i columns in condition that we swap A[i] and B[i]
  notswap: The cost of making both sequences increasing up to the first i columns in condition that we do not swap A[i] and B[i]
• Init : swap[0] = 1; notswap[0] = 0

class Solution(object):
    def minSwap(self, A, B):
        n = len(A)
        swap, notswap = [1001] * n, [1001] * n
        swap[0] = 1
        notswap[0] = 0

        for i in range(1, n):
            # Case 1 : strictly increasing, swap 2 or not
            if A[i-1] < A[i] and B[i-1] < B[i]:
                swap[i] = swap[i-1] + 1
                notswap[i] = notswap[i-1]

            # Case 2 : swap position i-1 or swap position i
            if A[i-1] < B[i] and B[i-1] < A[i]:
                swap[i] = min(swap[i], notswap[i-1] + 1)
                notswap[i] = min(notswap[i], swap[i-1])

        return min(swap[n-1], notswap[n-1])

• 我总是想记录上一个有没有swap，来record最优解，困于DFS的写法了！
• 跳开DFS的方式还是定义对DP的State，如果能想到定义两个State一个表示Swap一个表示不Swap，后面思路就很顺了！