Dynamic Programming Overview

Algorithms
dp
Catalogue
  1. 1. Overview
    1. 1.1. 1 问题引入Fibonacci
    2. 1.2. 2 核心思想
    3. 1.3. 3 动态规划题目特点
    4. 1.4. 4 动态规划组成部分

Overview

  • Big Name 公司必考，难度中上
  • 题目类型多，没有固定模板

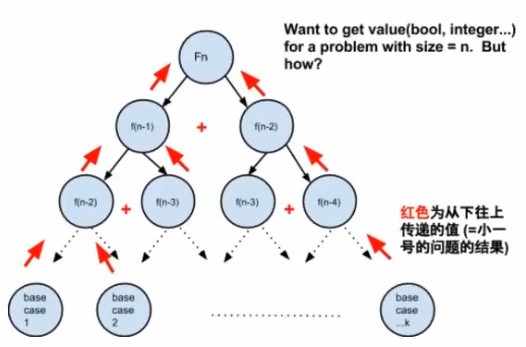
1 问题引入Fibonacci

  • F(n) = F(n-1) + F(n-1)
  • Base Case : F(0) = 0, F(1) = 1
1
2
3
4
public int fibN(int n) {
    if (n == 0 || n == 1) return n; // base case
    return fibN(n-1) + fibN(n-2); // recursice rule
}
1
2
3
4
5
6
7
8
9
10
11
public int fibN(int n) {
    int[] dp = new int[n+1];
    dp[0] = 0; // base case
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i-1] + dp[i-2];
        // dp[2] = dp[0] + dp[1]
        // dp[2] = dp[1] + dp[2];
    }
    return dp[n];
}

2 核心思想

类似于高中学习的数学归纳法

  1. 把一个大问题(size == n)的解决方案用比他小的问题(问题们)来解决，也就是思考从问题size=n-1增加到size=n的时候，如何用小问题的solution构建大问题的solution
  2. 与Recursion的关系
    • Recursion, 从大到小解决问题(自顶至下)，不记录任何sub-solution只考虑Base Case和Recursive Rule
    • DP, 从小到大解决问题(自底至上)，记录sub-solution
  3. 将计算中间结果保存下来，并改变计算顺序！

3 动态规划题目特点

  1. 计数
    • 有多少种方式走到右下角
    • 有多少种发发选出k个数使得和是Sum
  2. 求最大最小值
    • 从左上角走到右下角路径的最大数字和
    • 最长上升子序列长度
  3. 求存在性
    • 取石子游戏，先手是否必胜
    • 能不能选出k个数使得和是Sum

4 动态规划组成部分

  1. 确定状态
    • 解决动态规划的时候往往需要开一个数组，数组的每个元素f[i]或者f[i][j]代表什么物理意义(状态)
    • 研究最优策略的最后一步
    • 子问题
  2. 递推公式(转移方程)
    • 根据子问题定义直接得到
  3. 初始条件和边界情况
    • 细心，考虑周期
  4. 计算顺序
    • 利用之前的计算结果
Share