What is Union Find ?
- Union-Find算法(并查集算法)是解决动态连通性(Dynamic Conectivity)问题的一种算法,”人以类聚,物以群分”
- 一种用来解决集合查询合并的数据结构,支持 O(1)find, O(1)union
- 查询 Find
- 确定某个元素x属于哪一个集合
- 合并 Union
- 将两个集合合并
应用场景
- Computer Network
- 两个网络节点是否联通
- 最小的布线使得整个网络联通
- Social Network
- Linkedin 两个用户可能认识的人
- 集合论
Union Find vs DFS
在对问题进行建模的时候,我们应该尽量想清楚需要解决的问题是什么!
因为模型中选择的数据结构和算法显然会根据问题的不同而不同!
- Union Find - 给出两个节点,判断它们是否连通,如果连通,不需要给出具体的路径
- DFS - 给出两个节点,判断它们是否连通,如果连通,需要给出具体的路径
Algorithm
Quick-Find
有点类似于染色的过程,每个节点一个颜色,然后相同的节点设置成相同的颜色。
quick-find算法十分直观符合简单的思考过程。
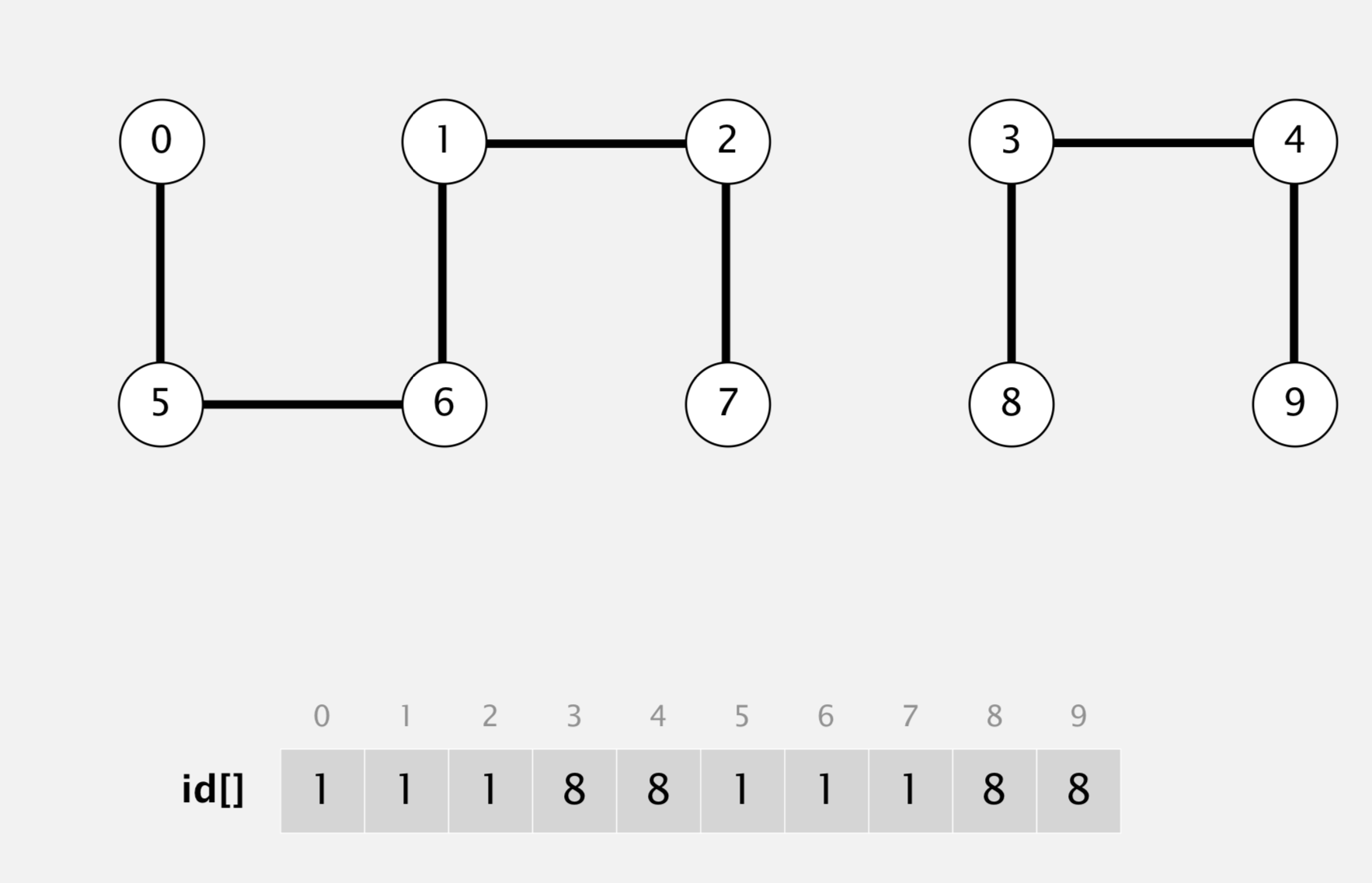
1 | # Time : O(1) |
每次添加新路径(Union)就是 “牵一发而动全身”,想要解决这个问题,关键就是要提高union方法的效率,让它不再需要遍历整个数组。
Quick-Union
- 以树的思想,表示集合!!!
- 这是UF算法里最关键的思路,以树的形式表示集合,这样组织正好可是很高效的实现find和union!

1 | # Time : O(Tree Height), Worst Case O(n) |
1 | # Time : O(Tree Height), Worst Case O(n) |
Weighted Quick-Union
既然树的高度成为制约时间复杂度的瓶颈,我们就想办法让树平衡!
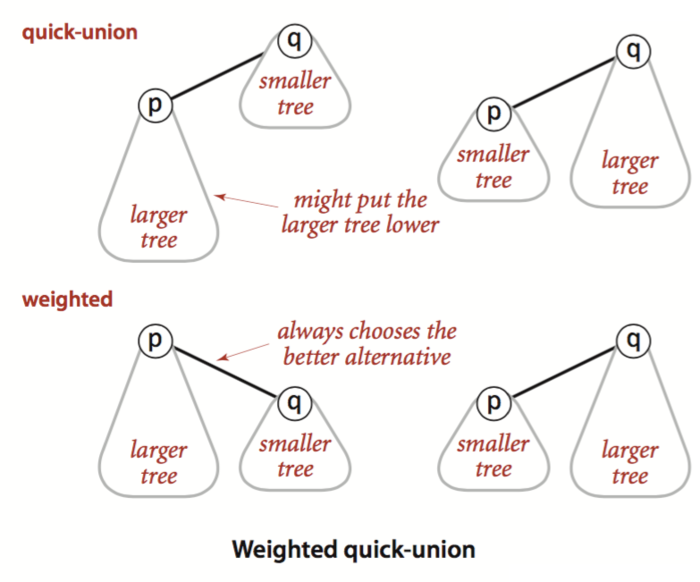
- 以Quick union为基础,我们 额外利用一个size[]保存每一个联通集中对象的数量。
- 在调用union()的时候,我们总是把 对象数目较少的联通集连接到对象数目较多的联通集 中。
- 通过这种方式,我们可以在一定程度上缓解树的高度太大的问题,从而改善Quick union的时间复杂度。
1 | # Time : O(logn) |
Path Compression
随着数据的增加,树的深度不断增加,性能会逐渐变差。这个时候,如果我们在计算一个node的root时,将node为根的树摘下来,挂在当前树的根结点上,会降低树的深度,也就是提高效率,降低时间复杂度。1
2
3
4
5
6
7
8
9# Path Compression 是在find的过程当中处理的
def find(x):
if root[x] == x:
return x
# make every other node in path point to its grandparent.
root[x] = find(root[x]) # Only one extra line
return root[x]
Weighted Quick-Union With Path Compression
Proof is very difficult, But the algorithm is still simple!
1 | # Weighted 是体现在Union的过程当中 |

Connected
查询两个元素是否在同一个集合内。
LintCode 589. Connecting Graph
Given n nodes in a graph labeled from 1 to n. There is no edges in the graph at beginning.
You need to support the following method:
- connect(a, b), add an edge to connect node a and node b.
- query(a, b), check if two nodes are connected
1 | class ConnectingGraph: |
LintCode 590. Connecting Graph II
- 统计每个联通块的元素个数
- query(a), Returns the number of connected component nodes which include node a.
1 | class ConnectingGraph2: |
130. Surrounded Regions
- 解法1 DFS
从边缘的’O’出发,通过DFS,所有能够遍历的’O’都可以暂时被标记为’#’,那么剩下未能被标记的’O’说明被surrounded,需要在遍历结束之后全部转为’X’
- 解法2 Union Find
将与边缘相连通的’O’全部union到一个dummy node(也可以用hasEdge[]来存储,不过内存占用更多,
最终将没有和这个dummy node是一个component的’O’点全部标记为’X1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46class UnionFind(object):
def __init__(self, n):
self.root = range(n)
def find(self, x):
root = self.root
if root[x] == x:
return x
root[x] = self.find(root[x])
return root[x]
def union(self, x, y):
root = self.root
rootx = self.find(x)
rooty = self.find(y)
if rootx != rooty:
# tip : 为了总是以dummy node(total)为父节点
root[min(rootx, rooty)] = max(rootx, rooty)
class Solution(object):
def solve(self, board):
if not board:
return
m, n = len(board), len(board[0])
total = m*n
uf = UnionFind(total+1)
grid = board
for i in xrange(m):
for j in xrange(n):
if grid[i][j] == 'X':
continue
# Connect to "total" root
if i == 0 or j == 0 or i == m-1 or j == n-1:
uf.union(total, i*n+j)
else:
d = [(1, 0), (0, 1), (-1, 0), (0, -1)]
for k in xrange(4):
ni, nj = i + d[k][0], j + d[k][1]
if grid[ni][nj] == 'O':
uf.union(ni*n + nj, i*n + j)
for i in xrange(m):
for j in xrange(n):
if grid[i][j] == 'X':
continue
if uf.find(i*n + j) != total:
grid[i][j] = 'X'
737. Sentence Similarity II
典型的Union Find 应用题,两个单词是不是similarity其实就是两个单词在不在同一个集合内(connected 操作)!
1 | class UnionFind(object): |
统计连通块的个数
the number of connected components.
LintCode 591. Connecting Graph III
- Query() - Returns the number of connected component in the graph
1 | class ConnectingGraph3: |
323. Number of Connected Components in an Undirected Graph
- 解法1. DFS
将Graph原本的nodes和edges表达形式,改成hash做的邻接表,这个就可以查询从每个节点出发到的节点!1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution(object):
def countComponents(self, n, edges):
visited = [0] * n
graph = [set() for _ in xrange(n)] # Adjacent Table
for i, j in edges:
graph[i].add(j)
graph[j].add(i)
res = 0
for i in xrange(n):
if visited[i] == 1:
continue
self.dfs(i, visited, graph)
res += 1
return res
def dfs(self, n, visited, graph):
if visited[n] == 1:
return
visited[n] = 1
for i in graph[n]:
self.dfs(i, visited, graph)
- 解法2. Union Find
1 | class Solution(object): |
305. Number of Islands II
实时放入island显示出联通块的个数,算是一个online的算法!
- 原始UF算法是一维的,2D坐标和1D坐标的转化
- 体现Union Find的Online特性,可以实时添加边!
1 | # Time : O(m * n + k) |
547. Friend Circles
1 | class Solution(object): |
Redundant Connection
261. Graph Valid Tree
1 | class Solution(object): |
684. Redundant Connection
1 | class Solution(object): |
685. Redundant Connection II
- Case1: There is a loop in the graph, and no vertex has more than 1 parent.
- 有环,且没有入度大于1的node => Union Find
- Case2: A vertex has more than 1 parent, but there isn’t a loop in the graph.
- 无环,且有入度大于2的node => last node (indegree > 1)
- Case3: A vertex has more than 1 parent, and is part of a loop.
- 有环,且有入度大于2的node
- 这种复杂的情况怎么筛选?
- Delete the second edge!
1 | class Solution(object): |