System Design - News Feed

2018-12-25

System Design

4S Analysis, Take “Design a Twitter” for example!

1S - Scenario

1 Enumerate Features

Register, Login
User Profile Display, Edit
Upload Image, Video
Search
Post, Share a tweet
Timeline, News Feed
Follow, Unfollow a user

2 Key Features

Post a Tweet
Timeline
News Feed
Follow, Unfollow a User
Register, Login

QPS Analysis & Predict

QPS(Query Per Second)

Concurrent User (Peak, Fast Growing)
Read QPS
Write QPS

Range of QPS

QPS = 100, one laptop enough
QPS = 1k, one Web Server (Single Point Failure)
QPS = 1m, 1000 Servers (Maintainance)
NoSQL(10k QPS Cassandra, 1M QPS Memcached)

2S - Service

Split/ Application/ Module

User Service
Tweet Service
Media Service
Friendship Service

3S - Storage

Schema/ Data/ SQL/ NoSQL/ File System
System = Service + Storage

1 Select Database

SQL Database
User Table, User Service
NoSQL Database
Tweets, Social Graph, Tweet Service
File System
Media

2 Design Schema

id & colums

News Feed

Facebook, Twitter, Wechat Moments, Byte Dance
Everyone has different news feed!!!
Follow and Unfollow

Pull Model

Merge K Sorted Arrays
News Feed, N Database Reads + Merge N arrays(Memory)
Post a tweet, 1 DB Write
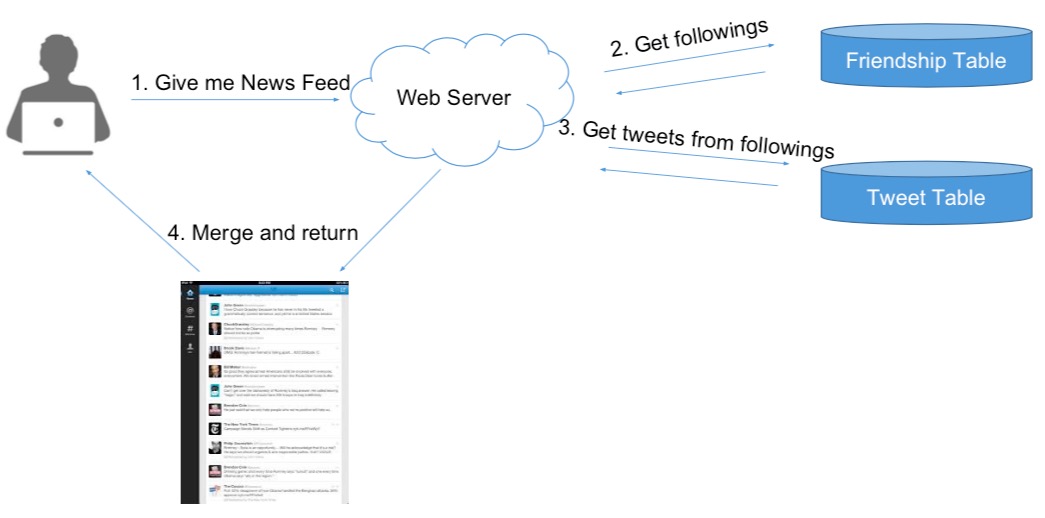
But it’s very slow to read N DB when you get your news feed!!!

Push Model

Fanout, When a user post a tweet, then push this tweet to every user who follow him or her
News Feed, 1 Database Reads
Post a tweet, N DB Writes(But user do not need to wait!!!)
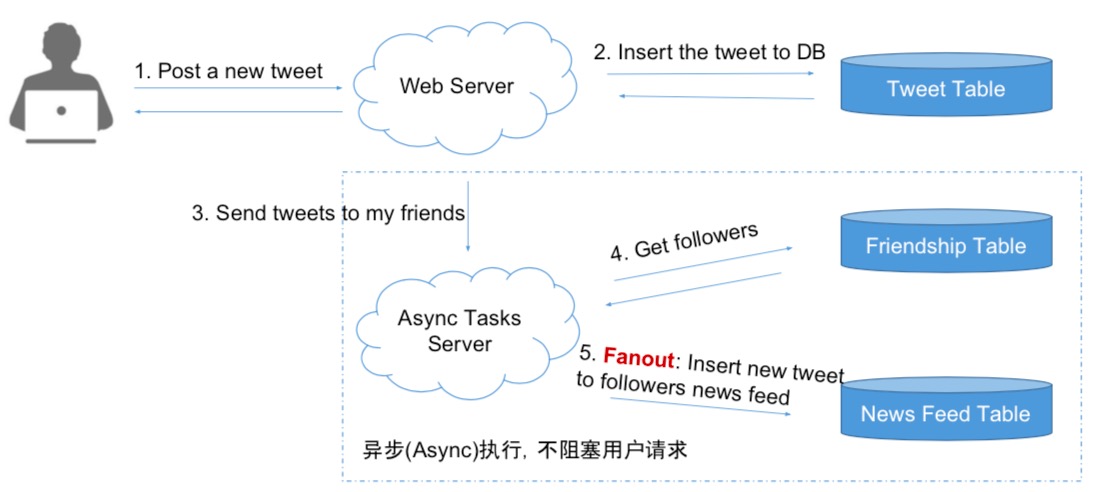
But when a user have toooo many followers, it take longer time to fanout!

Trade Off

Facebook - Pull
Instagram - Push + Pull
Twitter - Pull

4S - Scale

Sharding/ Optimize/ Special Case

Optimize

Pull Moedel

Cache before DB Query
Cache every user’s timeline
Cache every user’s news feed

Push Model

Disk is cheap
Inactive Users
Followers much larger than Following
Fanout will take several hours!!!
Seperate Star User and Normal User

Maintenance

(Explain it later!)

Robust
Scalability

Seperated Services

Follow and Unfollow
Likes
Thundering Herd

BFS Matrix

2018-12-03

Algorithms

bfs, matrix

490. The Maze

Directions BFS

class Solution(object):
    def hasPath(self, maze, start, destination):
        m, n = len(maze), len(maze[0])
        queue = collections.deque([(start)])
        visited = set()
        visited.add(tuple(start))
        dirs = [(0, 1), (1, 0), (-1, 0), (0, -1)]
        while queue:
            x, y = queue.popleft()
            if (x, y) == tuple(destination):
                return True
            for dx, dy in dirs:
                nx, ny = x, y
                while 0 <= nx + dx <= m-1 and 0 <= ny + dy <= n-1 and maze[nx+dx][ny+dy] == 0:
                    nx += dx
                    ny += dy

                if (nx, ny) not in visited:
                    queue.append((nx, ny))
                    visited.add((nx, ny))
        return False

296. Best Meeting Point

Solution1. Sort

Time : O(mn), Space : O(mn)
Only for this case that we do not have any obstacle and distance is Manhattan Distance

class Solution:
    def minTotalDistance(self, grid):
        xnums, ynums = [], []
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 1:
                    xnums.append(i)
                    ynums.append(j)

        return self.minDistance(xnums) + self.minDistance(ynums)

    def minDistance(self, nums):
        nums = sorted(nums)
        res = 0
        left, right = 0, len(nums)-1
        while left < right:
            res += nums[right] - nums[left]
            right -= 1
            left += 1
        return res

Solution2. BFS - TLE

Time : O($(mn)^2$), Space : O(mn)

More General Solution, But have high time complexity!!

class Solution:
    def minTotalDistance(self, grid):
        m, n = len(grid), len(grid[0])
        self.dis = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    self.bfs(grid, i, j)
        return min([self.dis[i][j] for i in range(m) for j in range(n)])

    def bfs(self, grid, i, j):
        queue = collections.deque([(i, j, 0)])
        visited = set([(i, j)])
        while queue:
            ni, nj, d = queue.popleft()
            self.dis[ni][nj] += d

            for di, dj in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                if (0 <= ni+di <= len(grid)-1 and
                    0 <= nj+dj <= len(grid[0])-1 and
                    (ni+di, nj+dj) not in visited):
                    queue.append((ni+di, nj+dj, d+1))
                    visited.add((ni+di, nj+dj))

317. Shortest Distance from All Buildings

Key idea : people to building or building to people ?

class Solution(object):
    def shortestDistance(self, grid):
        m, n = len(grid), len(grid[0])
        sums = collections.defaultdict(int)
        bcnt = collections.defaultdict(int)
        total = 0
        directions = [(-1,0), (0,-1), (0,1), (1,0)]
        for i in xrange(m):
            for j in xrange(n):
                if grid[i][j] == 1: # Run BFS
                    total += 1
                    visited = set()
                    queue = [(i,j,0)]
                    while queue:
                        x, y, val = queue.pop(0)
                        for dx, dy in directions:
                            if 0 <= x+dx <= m-1 and 0 <= y+dy <= n-1 and (x+dx, y+dy) not in visited and grid[x+dx][y+dy] == 0:
                                visited.add((x+dx, y+dy))
                                queue.append((x+dx, y+dy, val+1))
                                sums[(x+dx, y+dy)] += val+1
                                bcnt[(x+dx, y+dy)] += 1
        res = float('inf')
        for x, y in bcnt.keys():
            if bcnt[(x, y)] == total:
                res = min(res, sums[(x, y)])
        return -1 if res == float('inf') else res

where to add visited in BFS? when pop out or push in?
add visited hash set when you append an element in the queue!!!

class Solution(object):
    def shortestDistance(self, grid):
        if not grid:
            return -1

        m, n = len(grid), len(grid[0])
        matrix = [[[0, 0] for _ in range(n)] for _ in range(m)]
        cnt = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    self.bfs(matrix, i, j, grid)
                    cnt += 1
        res = float('inf')            
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 0 and matrix[i][j][1] == cnt:
                    res = min(res, matrix[i][j][0])
        return -1 if res == float('inf') else res

    def bfs(self, matrix, i, j, grid):
        m, n = len(grid), len(grid[0])
        queue = collections.deque([(i, j, 0)])
        visited = set()
        visited.add((i, j))
        while queue:
            x, y, step = queue.popleft()
            matrix[x][y][0] += step
            matrix[x][y][1] += 1
            for dx, dy in [(-1, 0), (0, -1), (1, 0), (0, 1)]:
                nx, ny = x+dx, y+dy
                if 0 <= nx <= m-1 and 0 <= ny <= n-1 and (nx, ny) not in visited and grid[nx][ny] == 0:
                    queue.append((nx, ny, step+1))
                    visited.add((nx, ny))

BFS

2018-12-02

Algorithms

bfs

Best First Search

Init state
expansion/generation rule
termination

301. Remove Invalid Parentheses

BFS - level order traversal
remove the minimum number

Solution1. BFS

class Solution(object):
    def removeInvalidParentheses(self, s):
        visited = set([s])
        queue = [s]
        res = []
        found = False
        while queue:
            for st in queue:
                if self.isValid(st):
                    found = True
                    res.append(st)

            if found: break
            nqueue = []
            for st in queue:
                for i, ch in enumerate(st):
                    if ch in "()":
                        nst = st[:i]+st[i+1:]
                        if nst not in visited:
                            nqueue.append(nst)
                            visited.add(nst)
            queue = nqueue
        return res

    def isValid(self, s):
        left = 0
        for ch in s:
            if ch == '(':
                left += 1
            elif ch == ')':
                left -= 1
                if left < 0:
                    return False
        return left == 0

We can also use dfs with pruning to solve this problem!

Solution2. DFS + pruning

Backtracking

class Solution(object):
    def removeInvalidParentheses(self, s):
        lp = rp = 0
        for ch in s:
            if ch == '(':
                lp += 1
            elif ch == ')':
                if lp > 0:
                    lp -= 1
                else:
                    rp += 1
        res = set()
        self.dfs(lp, rp, 0, s, [], res)
        return list(res)

    def dfs(self, lp, rp, pairs, s, path, res):
        if lp < 0 or rp < 0 or pairs < 0:
            return

        if len(s) == 0:
            if lp == 0 and rp == 0 and pairs == 0:
                res.add(''.join(path))
            return

        if s[0] == '(':
            self.dfs(lp-1, rp, pairs, s[1:], path, res)
            self.dfs(lp, rp, pairs+1, s[1:], path + [s[0]], res)
        elif s[0] == ')':
            self.dfs(lp, rp-1, pairs, s[1:], path, res)
            self.dfs(lp, rp, pairs-1, s[1:], path + [s[0]], res)
        else:
            self.dfs(lp, rp, pairs, s[1:], path + [s[0]], res)

Graph Cycle

2018-12-01

Algorithms

graph

Detect the Cycle

Find if a cycle exits in a graph

261. Graph Valid Tree

Undirected Graph: Union Find, DFS, BFS

Solution1. Union Find

graph is represented by edges!!! signal to use union find!!!

tree is connected graph without cycle, but graph can be seperate clusters!!!

class Solution(object):
    def validTree(self, n, edges):
        root = range(n)
        self.cnt = n
        def find(x):
            if root[x] == x:
                return x
            root[x] = find(root[x])
            return root[x]

        def union(x, y):
            rootx = find(x)
            rooty = find(y)
            if rootx != rooty:
                root[rootx] = rooty
                self.cnt -= 1
                return True
            return False

        for i, j in edges:
            if not union(i, j):
                return False
        return self.cnt == 1

solution2. DFS

for undirected graph, it’s better to use Union Find and BFS
prev node !!!!
3 states for visited: 0-no visited，1-visiting，2-visited

class Solution(object):
    def validTree(self, n, edges):
        graph = collections.defaultdict(set)
        for i, j in edges:
            graph[i].add(j)
            graph[j].add(i)

        visited = [0] * n
        if not self.dfs(-1, 0, visited, graph):
                return False
        return (0 not in visited)

    def dfs(self, prev, i, visited, graph):
        if visited[i] == 2:
            return True

        if visited[i] == 1:
            return False

        visited[i] = 1

        for nei in graph[i]:
            if nei == prev:
                continue
            if not self.dfs(i, nei, visited, graph):
                return False

        visited[i] = 2
        return True

Solution3. BFS

prev node to avoid edge(a, b) and (b, a) cycle !!!

class Solution(object):
    def validTree(self, n, edges):
        graph = collections.defaultdict(set)
        for i, j in edges:
            graph[i].add(j)
            graph[j].add(i)

        visited = [0] * n
        queue = collections.deque([(0, -1)])
        while queue:
            node, prev = queue.popleft()
            visited[node] = 1
            for nei in graph[node]:
                if nei == prev:
                    continue
                if visited[nei]:
                    return False
                queue.append((nei, node))
        return sum(visited) == n

Directed graph

207. Course Schedule

Directed graph: DFS, BFS

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses.

Solution1. DFS
visited三种状态，-1正在visit, 0未visit, 1已经visit

Why 三种状态？or 两种状态？
- 两种状态，做DFS时间复杂度是O(n^2)
- 引入第三种状态，可以避免访问已经访问过不构成环的点，O(n)

# Time : O(n)
class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        graph = collections.defaultdict(set)
        for c, p in prerequisites:
            graph[c].add(p)

        visited = [0] * numCourses

        for i in xrange(numCourses):
            if not self.dfs(i, visited, graph):
                return False
        return True

    def dfs(self, i, visited, graph):
        if visited[i] == 1:
            return True

        if visited[i] == -1:
            return False

        visited[i] = -1

        for edge in graph[i]:
            if not self.dfs(edge, visited, graph):
                return False

        visited[i] = 1
        return True

Solution2. BFS

有向图的BFS算法还是比较有意思的，基于indegree的！
Indegree, 每次访问入度为0的节点，并删掉所在边，最后sum(indegree) == 0!

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        graph = [[] for _ in xrange(numCourses)]
        indegree = [0] * numCourses
        for i, j in prerequisites:
            graph[j].append(i)
            indegree[i] += 1

        queue = [i for i in xrange(numCourses) if indegree[i] == 0]
        while queue:
            course = queue.pop(0)
            for n in graph[course]:
                indegree[n] -= 1
                if indegree[n] == 0:
                    queue.append(n)
        return sum(indegree) == 0

Graph => Tree

684. Redundant Connection

union find

class Solution(object):
    def findRedundantConnection(self, edges):
        n = len(edges)
        root = range(n+1)

        def find(x):
            if root[x] == x:
                return x
            root[x] = find(root[x])
            return root[x]

        for src, dst in edges:
            root1 = find(src)
            root2 = find(dst)
            if root1 != root2:
                root[root1] = root2
            else:
                return [src, dst]

685. Redundant Connection II

class Solution(object):
    def findRedundantDirectedConnection(self, edges):
        candidates = []
        n = len(edges)
        parent = {}
        for i, (p, c) in enumerate(edges):
            if c in parent:
                candidates = [(parent[c], c), (p, c)]
                edges[i][0] = 0
            else:
                parent[c] = p

        # candiates is none => only cycle case
        # else => indegree > 1 case

        root = range(n+1)
        def find(x):
            if x == root[x]:
                return x
            root[x] = find(root[x])
            return root[x]

        for p, c in edges:
            root1 = find(c)
            root2 = find(p)
            if root1 == root2:
                if not candidates:
                    return [p, c]
                else:
                    return candidates[0]
            root[root1] = root2
        return candidates[1]

DP - Sequence Adjacent Element

2018-11-27

Algorithms

dp

256. Paint House

class Solution(object):
    def minCost(self, costs):
        if not costs:
            return 0

        n = len(costs)
        dp = [[0] * 3 for _ in range(n)]
        for j in range(3):
            dp[0][j] = costs[0][j]

        for i in range(1, n):
            for j in range(3):
                dp[i][j] = costs[i][j] + min(dp[i-1][j-1], dp[i-1][j-2])
        return min(dp[-1])

265. Paint House II

class Solution(object):
    def minCostII(self, costs):
        if not costs:
            return 0

        n, k = len(costs), len(costs[0])
        dp = [[0] * k for _ in range(n)]
        for j in range(k):
            dp[0][j] = costs[0][j]

        for i in range(1, n):
            for j in range(k):
                dp[i][j] = costs[i][j] + min(dp[i-1][:j] + dp[i-1][j+1:])
        return min(dp[-1])

276. Paint Fence

class Solution(object):
    def numWays(self, n, k):
        if n == 0 or k == 0:
            return 0

        dp = [[0] * 2 for _ in range(n)]
        dp[0][0] = k
        dp[0][1] = 0
        for i in range(1, n):
            dp[i][0] = (dp[i-1][0] + dp[i-1][1]) * (k-1)
            dp[i][1] = dp[i-1][0]
        return sum(dp[-1])

198. House Robber

class Solution(object):
    def rob(self, nums):
        if not nums:
            return 0

        n = len(nums)
        dp1 = [0] * n # Stole
        dp2 = [0] * n # Not Stole
        dp1[0] = nums[0]
        for i in range(1, n):
            dp1[i] = dp2[i-1] + nums[i]
            dp2[i] = max(dp1[i-1], dp2[i-1])
        return max(dp1[-1], dp2[-1])

213. House Robber II

class Solution(object):
    def rob(self, nums):
        n = len(nums)
        if n <= 1:
            return sum(nums)

        prev = rob1 = 0
        for num in nums[1:]:
            temp = rob1
            rob1 = max(prev + num, rob1)
            prev = temp

        prev = rob2 = 0
        for num in nums[:-1]:
            temp = rob2
            rob2 = max(prev + num, rob2)
            prev = temp

        return max(rob1, rob2)

Calculator

2018-11-23

Algorithms

stack, topic

150. Evaluate Reverse Polish Notation

Stack, Reverse Polish Notation

class Solution(object):
    def evalRPN(self, tokens):
        stack = []
        for token in tokens:
            if token in "+-*/":
                n2 = stack.pop()
                n1 = stack.pop()
                if token == '+':
                    temp = n1 + n2
                elif token == '-':
                    temp = n1 - n2
                elif token == '*':
                    temp = n1 * n2
                else:
                    temp = n1 / n2
                    if n1 * n2 < 0 and n1 % n2 != 0:
                        temp += 1
                stack.append(temp)
            else:
                stack.append(int(token))
        return stack.pop()

Serialization

2018-11-17

Algorithms

string, topic, tree

Tree <-> String

When you use network to transport a tree or a graph, you can not pass the momery. So usually you have to use a string to transport!

Binary Search Tree
Complete Tree

Full Tree

297. Serialize and Deserialize Binary Tree

class Codec:
    def serialize(self, root):
        res = []
        def dfs(node):
            if not node:
                res.append("None")
                return

            res.append(str(node.val))
            dfs(node.left)
            dfs(node.right)
        dfs(root)
        return ','.join(res)



    def deserialize(self, data):
        def helper(q):
            if tokens[0] == "None":
                q.popleft()
                return None
            root = TreeNode(q.popleft())
            root.left = helper(q)
            root.right = helper(q)
            return root

        tokens = collections.deque(data.split(','))
        root = helper(tokens)
        return root

Tree Serialization

426. Convert Binary Search Tree to Sorted Doubly Linked List

O(n) extra space

# Time : O(n), Space : O(n)
class Solution(object):
    def treeToDoublyList(self, root):
        if not root:
            return None

        res = []
        self.inOrder(root, res)
        n = len(res)
        for i in xrange(n):
            res[i].right = res[i+1] if i < n-1 else res[0]
            res[i].left = res[i-1]
        return res[0]

    def inOrder(self, root, res):
        if not root:
            return
        self.inOrder(root.left, res)
        res.append(root)
        self.inOrder(root.right, res)

in-place

# Time : O(n), Space : O(1)
class Solution(object):
    def treeToDoublyList(self, root):
        if not root:
            return None

        self.prev = None
        self.head = None
        self.inOrder(root)
        self.prev.right = self.head
        self.head.left = self.prev
        return self.head

    def inOrder(self, root):
        if not root:
            return
        self.inOrder(root.left)
        if self.prev:
            root.left = self.prev
            self.prev.right = root
        else:
            self.head = root
        self.prev = root
        self.inOrder(root.right)

Tree De-Serialization

We can NOT construct a Binary Tree using postorder and preorder

106. Construct Binary Tree from Inorder and Postorder Traversal

Global Question divide to sub problem

class Solution(object):
    def buildTree(self, inorder, postorder):
        if not inorder or not postorder:
            return None

        root = TreeNode(postorder.pop())
        inorderindex = inorder.index(root.val)
        root.right= self.buildTree(inorder[inorderindex+1:], postorder)
        root.left = self.buildTree(inorder[:inorderindex], postorder)

        return root

105. Construct Binary Tree from Preorder and Inorder Traversal

class Solution(object):
    def buildTree(self, preorder, inorder):
        if (not preorder) or (not inorder):
            return None
        root=TreeNode(preorder.pop(0))
        ro=inorder.index(root.val)
        root.left=self.buildTree(preorder,inorder[:ro])
        root.right=self.buildTree(preorder,inorder[ro+1:])
        return root

Construct Binary Tree from Inorder and level Order

114. Flatten Binary Tree to Linked List

class Solution(object):
    def flatten(self, root):
        if not root:
            return

        if not root.left:
            self.flatten(root.right)
            return

        self.flatten(root.left)
        self.flatten(root.right)

        cur = root.left
        while cur.right:
            cur = cur.right
        cur.right = root.right
        root.right = root.left
        root.left = None

Monotone Stack

2018-11-15

Algorithms

stack

Next Greater Element

496. Next Greater Element I

class Solution(object):
    def nextGreaterElement(self, findNums, nums):
        dic = {}
        stack = []
        for num in nums:
            while stack and num > stack[-1]:
                dic[stack.pop()] = num
            stack.append(num)

        res = []
        for num in findNums:
            if num not in dic:
                res.append(-1)
            else:
                res.append(dic[num])
        return res

503. Next Greater Element II

class Solution(object):
    def nextGreaterElements(self, nums):
        n = len(nums)
        res = [-1] * n
        stack = []
        for i in range(n):
            while stack and nums[stack[-1]] < nums[i]:
                res[stack.pop()] = nums[i]
            stack.append(i)

        for i in range(n):
            while stack and nums[stack[-1]] < nums[i]:
                res[stack.pop()] = nums[i]
        return res

84. Largest Rectangle in Histogram

Solution1. middle heart open flower

for each index i, walk right to find the left border and right border.
Time = O($n^2$)

Solution2. Stack

Use a Stack to store all the indices of the columns that form an ascending order stack that stores the indeices in ascending order. [1, 5, 6
When scanning the element with index = 4, M[4] = 2 < M[3] = 6, so we keep checking left column of index 4, and calculate the area of index 3,2 and pop them out of the stack, after this step, the stack is [1, 5
Priciple, to maintain the stack to make sure the colums shose indices are stored in the stack from an sacending order.
TimeO(n), because every single element can only be inserted and popped out of the stack once and only once.

class Solution(object):
    def largestRectangleArea(self, heights):
        stack = []
        hs = heights + [0]
        i = 0
        res = 0
        while i <= len(hs)-1:
            if not stack or hs[stack[-1]] < hs[i]:
                stack.append(i)
                i += 1
            else:
                idx = stack.pop()
                res = max(res, hs[idx] * (i if not stack else (i-stack[-1]-1)) )
        return res

42. Trapping Rain Water

class Solution(object):
    def trap(self, height):
        n = len(height)
        stack = []
        res = 0
        i = 0
        while i <= n-1:
            if not stack or height[i] <= height[stack[-1]]:
                stack.append(i)
                i += 1
            else:
                t = stack.pop()
                if not stack:
                    continue
                res += (min(height[stack[-1]], height[i]) - height[t]) * (i - stack[-1] - 1)
        return res

Interval Problem

2018-11-14

Algorithms

topic

Range

370. Range Addition

Trade off for Update and Query!

O(1) for update and O(n) for Query
O(n) for update and O(1) for Query
We only care about the intervals start and end!!!

class Solution(object):
    def getModifiedArray(self, length, updates):
        nums = [0] * length
        for start, end, diff in updates:
            nums[start] += diff
            if end < length - 1:
                nums[end+1] -= diff

        for i in range(1, length):
            nums[i] += nums[i-1]
        return nums

Overlap

How to define two intervals overapped?

A.end > B.start
B.end > A.start

Why we always sort by start or end at first?

252. Meeting Rooms

class Solution:
    def canAttendMeetings(self, intervals):
        intervals.sort(key=lambda x:x.start)
        for i in range(1, len(intervals)):
            if intervals[i].start < intervals[i-1].end:
                return False
        return True

253. Meeting Rooms II

class Solution(object):
    def minMeetingRooms(self, intervals):
        times = []
        for interval in intervals:
            times.append((interval.start, 1))
            times.append((interval.end, 0))
        times.sort()
        res = 0
        cnt = 0
        for time, fg in times:
            cnt += 1 if fg == 1 else -1
            res = max(res, cnt)
        return res

Follow Up : Return Max Overlapped Interval

Operations

56. Merge Intervals

# Definition for an interval.
# class Interval(object):
#     def __init__(self, s=0, e=0):
#         self.start = s
#         self.end = e

class Solution(object):
    def merge(self, intervals):
        if not intervals:
            return []

        intervals.sort(key = lambda x:x.start)
        n = len(intervals)
        stack = [intervals[0]]
        for i in range(1, n):
            start, end = intervals[i].start, intervals[i].end
            if start <= stack[-1].end:
                stack[-1].end = max(stack[-1].end, end)
            else:
                stack.append(intervals[i])
        return stack

57. Insert Interval

O(n)

class Solution(object):
    def insert(self, intervals, newInterval):
        n = len(intervals)
        res = []
        i = 0
        while i < n and newInterval.start > intervals[i].end:
            res.append(intervals[i])
            i += 1

        while i < n and intervals[i].start <= newInterval.end:
            newInterval.start = min(intervals[i].start, newInterval.start)
            newInterval.end = max(intervals[i].end, newInterval.end)
            i += 1
        res.append(newInterval)

        while i < n:
            res.append(intervals[i])
            i += 1

        return res

System Design Introduction

2018-11-13

System Design

System/Solution/Product Design

Design a Twitter?
Design a Uber?
Design a short URL service.
Product -> functionalities/use cases -> Architecture

Topic

Storage

Distributed file system
Distributed database
Computation
Batch Processing
Streaming Processing
Web Application

Data Center

Cluster
Rack
Node/Server(many computers)
Distributed File System

Use file system interfaces to manage your data (files and directions)
Data is distributed in many machies
Examples: GFS(Google File System), HDFS, Ceph FS, GlusterFS, MapR FS…
When to use a DFS?

Durability

Hadoop Distributed File system

Key features/assumptions

Scale up to 100+ PB of storage and a single cluster of several thousand servers,
supporting close to a billion files and blocks

Designed to run on commodity hardware

some components of HDFS is always non-functional

Architecture

1S - Scenario

1 Enumerate Features

2 Key Features

QPS Analysis & Predict

2S - Service

3S - Storage

1 Select Database

2 Design Schema

News Feed

Pull Model

Push Model

Trade Off

4S - Scale

Optimize

Pull Moedel

Push Model

Maintenance

Seperated Services

Solution1. Sort

Solution2. BFS - TLE

Best First Search

Solution1. BFS

Solution2. DFS + pruning

Detect the Cycle

Solution1. Union Find

solution2. DFS

Solution3. BFS

Directed graph

Solution1. DFS

Solution2. BFS

Graph => Tree

Tree <-> String

Tree Serialization

Tree De-Serialization

Construct Binary Tree from Inorder and level Order

Next Greater Element

Solution1. middle heart open flower

Solution2. Stack

Range

Overlap

Operations

Topic

Storage

Computation

Web Application

Data Center

Distributed File System

Hadoop Distributed File system